Ray Aiming is an iterative ray tracing algorithm used in optical design work to find rays in object space that correctly fill the given aperture size. This article will introduce the usage of Ray Aiming and Pupil Aberration in CAXCAD:
Ray Aiming
Ray Aiming is an iterative ray tracing algorithm used in optical design work to find rays in object space that correctly fill the given aperture size. Typically, Ray Aiming is only necessary when there is significant aberration or displacement/tilt of the pupil (the image of the aperture as seen from object space). Without Ray Aiming, actual rays from the object are aimed at the paraxial entrance pupil, the location and size of which can be found in the data report. In many cases, aiming at the entrance pupil will not adversely affect the system. Users should investigate and use Ray Aiming only when necessary!
Pupil Aberration
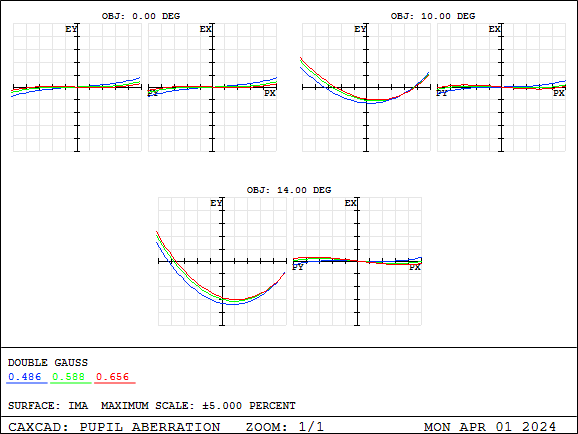
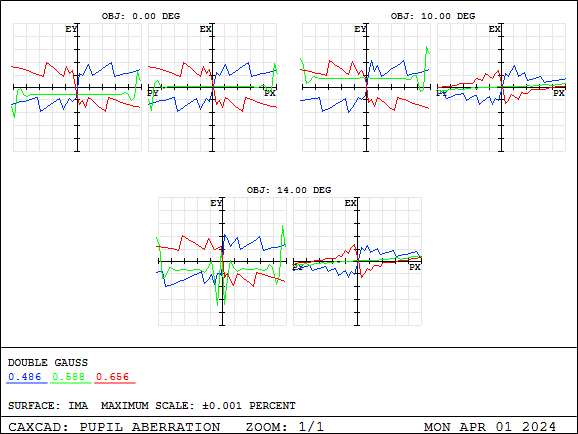
Pupil aberration is defined as the difference between the real ray intercept on the aperture surface and the on-axis primary wavelength paraxial ray intercept, expressed as a percentage of the paraxial aperture radius. If the maximum aberration exceeds a few percent, Ray Aiming may be required to correctly fill the aperture surface with rays in object space. If Ray Aiming is enabled, the pupil aberration will appear to be zero (or a very small residual value) because the distortion is accounted for by the ray tracing algorithm. This serves as a check to verify that Ray Aiming is working correctly. The definition used here for pupil aberration is not intended to be complete or consistent with other definitions. The sole purpose of this feature is to provide guidance on whether Ray Aiming is required.
Below, we demonstrate the usage of Ray Aiming with an example. Open the classic double Gauss lens and observe the position of the pupil, especially the convergence of rays at the edges.

Use magnification to display the rays at the edge of the cable, and it will be found that the rays from different fields of view do not converge perfectly at the edge of the aperture STOP. In this case, there is pupil aberration in the optical system.

By analyzing pupil aberration, it can be determined that the percentage value of pupil aberration is within 5%, which is generally an acceptable value because this lens is not a wide-angle lens.
Ray Aiming 01: CX Ray Aiming
CX Ray Aiming is a unique aiming algorithm in CAXCAD. When this feature is enabled, the field of view needs to be increased with a vignette, and subsequent rays do not need iterative calculation. This is the fastest way, especially for lens optimization, with very high efficiency.
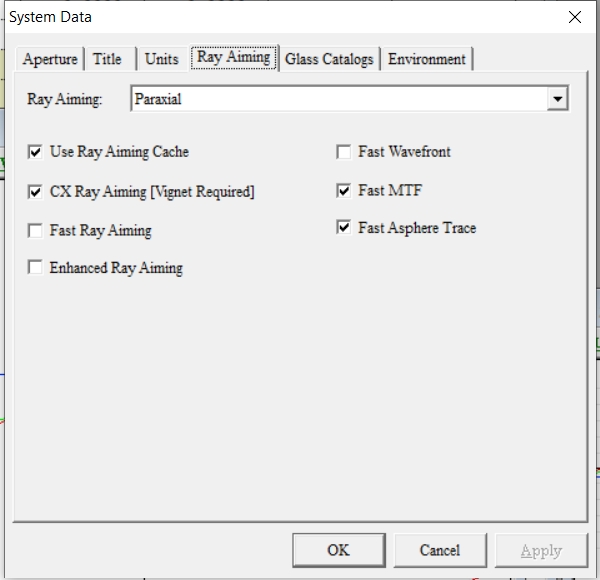
Enable the vignette.
Ray Aiming 02: Fast Ray Aiming
This is a fast Ray Aiming algorithm. During system updates, only a very small amount of iterative calculation is required for the rays, and subsequent ray tracing does not require iteration. Therefore, this method still maintains high efficiency, but the accuracy is higher.
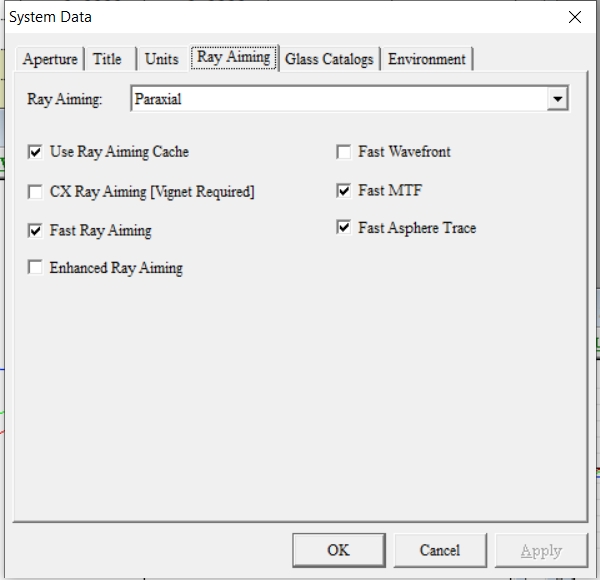
Rays on the edge of the pupil can be quickly aimed.
Pupil aberration also drops to within 0.5%.
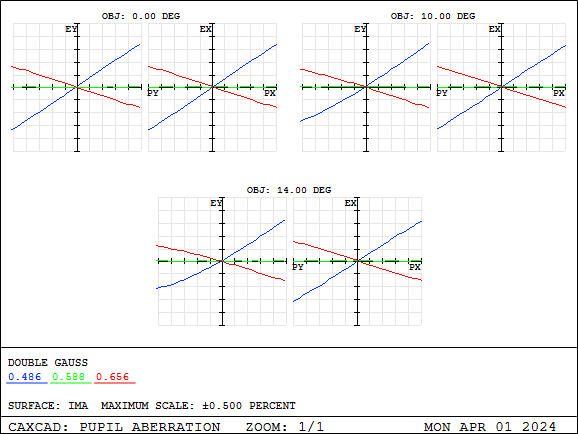
When the image is magnified again, we will find that there is still an error here.

Ray Aiming 03: Enhanced Ray Aiming
This is a ray tracing algorithm for Ray Aiming, so it is the least efficient in terms of computational efficiency. It is not recommended to use this method, but when the first two methods cannot meet the requirements, this one can be chosen. This algorithm can guarantee the highest accuracy.
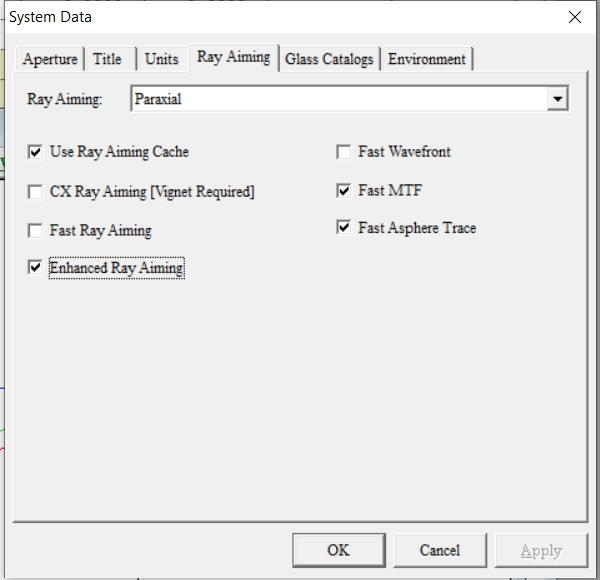
Enable the Enhanced method, and the aiming accuracy can reach 1e-5.
Rays are usually accurately aimed.
summary:
This article introduces three ray aiming functionalities of the CAXCAD optical design software, along with their respective characteristics and advantages.
Firstly, CX Ray Aiming is an innovative technology unique to CAXCAD. When combined with vignetting, it enables rapid tracing of optical systems, thus enhancing the speed of lens analysis and optimization.
The other two functionalities can be chosen based on specific user needs. Pupil aberrations provide analytical functionality for this option.

